Description

题目传送门：P10692 [SNCPC2024] 表达式矩阵。

构造一个 $n \times m$ 的矩阵，其中每个位置要么是 $1$，要么是 $\tt +$ 或者 $\tt ∗$，使得在满足每一行每一列均为一个合法表达式的前提下，最小化每一行、每一列表达式的值之和。

Analysis（转自官方题解）

  • 对于行列大小均为偶数的情况，以 $6\times 8$ 为例答案形如:

注意到每行 $/$ 每列恰有一个 $11$。由于无法构造出只含 $1$ 的解，显然使用乘号连接 $11$ 和 $1$ 是最优的。

  • 对于列大小为奇数的情况，以 $6 × 9$ 为例如：

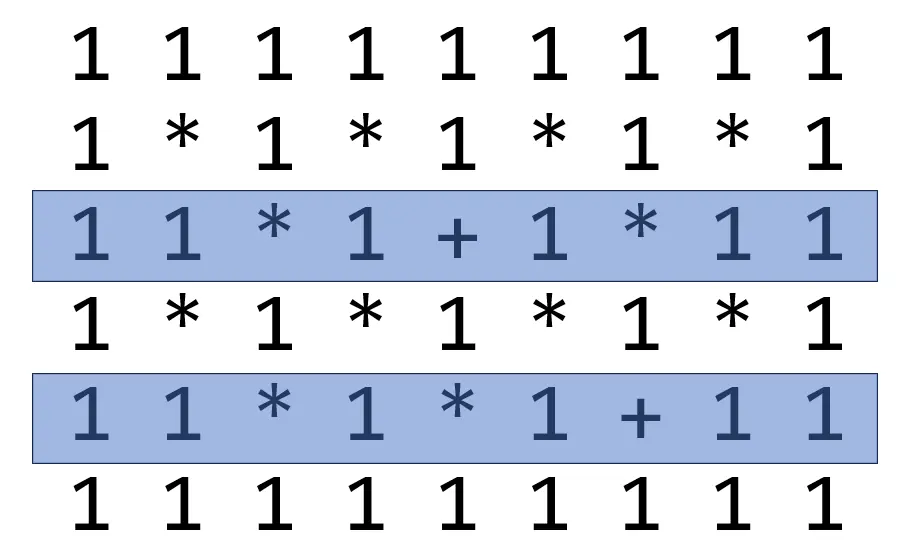
所有包含两个 $11$ 的行都必须使用一个 $+$，否则会产生 $11 \times 11$ 的结果，这是我们不能接受的。

同时，除此之外每多使用一个 $+$，都会使答案增加，所以只需要在这些行中选恰好一个运算符改为 $+$ 即可。

行大小为奇数的情况类似。

  • 对于行列大小均为奇数的情况，以 $7 × 9$ 为例：

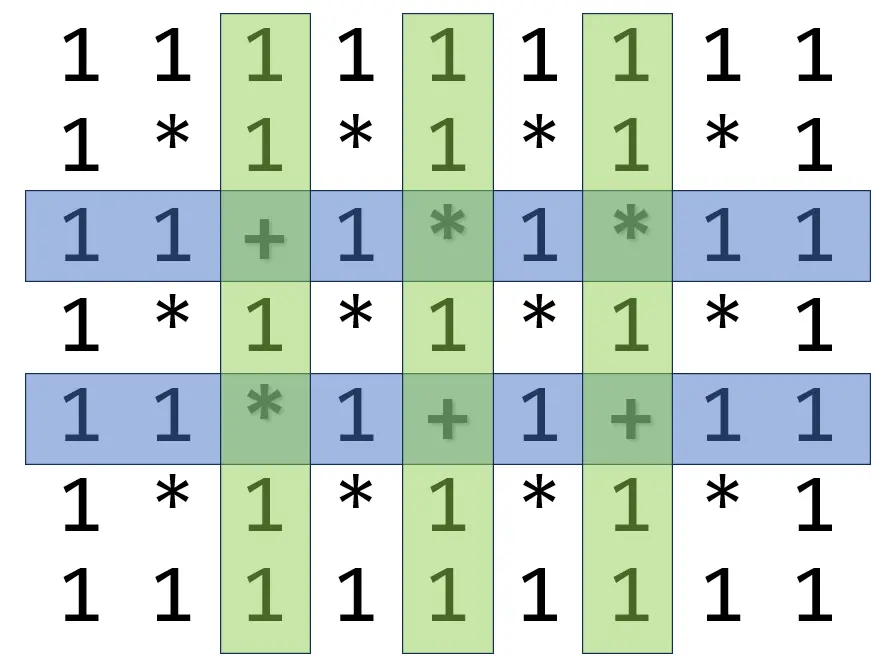
所有包含两个 $11$ 的行都必须使用一个 $+$，所有包含两个 $11$ 的列都必须使用一个 $+$。

如图所示，观察位于交点的六个运算符，需要保证每行都有一个 $+$，每列都有一个 $+$。可以考虑斜着分配。

通过搜索和合理的剪枝，能在可接受的时间内算出答案。

考虑答案空间只有 $9 × 9$，可以搜出所有的答案硬编写在代码中。